Modern sports science in context of bio-informatics, mathematics and chaos theory
Фотографии:
ˑ:
Professor, Dr.Biol. S.I. Loginov
Surgut State University, Surgut
Keywords: sport science, determinism, stochastic chaos.
Introduction. Computer science is renowned as a subdiscipline of cybernetics and currently appears as an independent branch of science, the basics of which were developed by Claude Elwood Shannon in the 1950s [10]. From its origin to the present day, computer science deals with mathematic analysis and development of methods for communication, storage, classification and processing of information in all fields of science, including sport science. Besides, bio-informatics, the subdiscipline of computer science, is the major factor in modernization of the educational process organization; its principles were echoed in the articles in Teoriya i praktika fizicheskoy kultury, the top scientific journal contributing to sport science development, which can hardly be overestimated. However, information cannot be collected and stored without a purpose. Its communication is rational and determined. Determinism theory, that has long been identifying the complex scientific concept of the world, is based on cause-and-effect relations, in which every event or action is preconditioned by a certain factor. In case there is no evident cause, it should be detected and analyzed. The search for causes has been an object of scientific investigation over many centuries. It laid out the foundation for the philosophical research on causality. The pioneering works are considered to be Johannes Kepler’s laws of planetary motion (1609, 1618) [13] and the writings of Galileo Galilei (1623) [1]. In particular, Galilei remarks, “Philosophy is written in this grand book, the universe, which stands continually open to our gaze. But the book cannot be understood unless one first learns to comprehend the language and read the letters in which it is composed. It is written in the language of mathematics, and its characters are triangles, circles, and other geometric figures...” [1: p. 131]. Galileo Galilei is justly referred to as one of the founders of classical mechanics, an area of science that made the study of the motion of bodies its cornerstone.
Objective of the study was to provide justification for modern sport science development in terms of deterministic chaos and nonlinearity of complex and dynamic biological systems.
Results and discussion. The principles of causality stem from the ideas of René Descartes, the first major figure in the philosophical movement known as rationalism. In the Third Meditation, originally published in 1641, Descartes points out that the principle of causality is irrefutable, cannot be confirmed by experience, since it is an axiom, which precedes the experience. For instance, in physics, the principle is considered a priori and states: “Every effect has a cause” [12]. Regarding the calculation of planets’ trajectories, Isaac Newton asserted that the concepts of “initial conditions” and “law of motion” should be considered separately (1687). Newton simplified the model and assumed that every planet is singly related to the sun. Newton’s calculation was similar to that of the Kepler’s laws [14]. Isaac Newton developed the method of differential calculus, discovered the universal law of gravitation and launched the entire epoch of classical physics, which lasted until the impact of the needs for relativistic and quantum physics in the 20th century. However, this was relevant to local determinism, which concerns a finite number of elements. A good illustration would be ballistics, projectile motion and trajectory calculations. Universal determinism, also called “déterminisme Laplacien”, remains problematic, since consideration of the universe in its totality as a deterministic system is a thorny issue by default. Nevertheless, Pierre-Simon Laplace, French mathematician and astronomer, stated the concept of universal determinism most clearly in 1778 [4]. He proved that the totality of celestial body motions (the sun and the planets) could be explained by the laws of Newton, reducing the study of planets to a series of differential equations.
Within physics and physiology, the recent mathematical models included the idea that many phenomena cannot be predicted precisely, but can be partly determined in light of the chaos theory [2, 11]. These models can be characterized as having sensitivity to initial conditions, fractal dimensions and acting as strange attractors [6, 9].
Scientists frequently attempt to interpret the natural phenomena on the basis of mathematical models. However, it appears that the abstract equations constructed by the human mind are considered to be adequate representation of reality, while the congruity of the mind and environment stands for the ultimate achievement of mankind. Refutation through experimental studies, i.e. falsification, is typical for scientific theories, whereas mathematical models are non-contradictory (in terms of mathematical logic) and deduced from a number of axioms. In the modern context, physicists, biologists and researchers in the field of sport medicine tend to interpret the natural phenomena in view of mathematical models, which is rarely justified, since the body of an athlete is a complex and dynamic system characterized by chaotic behavior. We shall briefly consider the formation of the concepts of dynamic systems, phase space, fractal dimensions and other properties of complex biological systems.
Andrey Nikolaevich Kolmogorov, one of the most prominent mathematicians of the 20th century, made a great contribution to the study of the probability theory, turbulence, information theory, and topology. His pioneering works are associated with many other significant scientific achievements. In 1954, he reconsidered the mathematical research of Henri Poincaré. The same was pursued by Jürgen Kurt Moser in 1962 and Vladimir Igorevich Arnold in 1963. Kolmogorov proved that quasi-periodic regular motion persists in an integrable system even if a small perturbation is applied. The Kolmogorov–Arnold–Moser theorem (KAM theorem) thus gives mathematical bounds for integrability and basically describes a progressive transition to chaos, inasmuch as all trajectories are regular and quasi-periodic within the integrable system.
In case of one slight perturbation there is still a probability to observe the quasi-periodic behavior within a random point in the phase space. When a more significant perturbation is applied, the probability of quasi-periodic behavior decreases, while the chaotic trajectories increase till the ultimate chaotic behavior is reached. In terms of total chaos, the only constant element is the motion of energy, which is known as ergodic motion. A.N. Kolmogorov founded the Russian school of mathematical sciences, which made a significant contribution to the development of the ergodic theory of statistics and research on dynamic complex system [3]. The integrability of a system was proved. In mathematics, it relates to the differential equations that have solutions; in mechanics – to the quasi-periodic systems; hence the definition: dynamic system is the system, which unfolds over time depending upon variables or in a deterministic manner; the outcome is contingent on the previous events (the past) and actual causes (the present) with every initial state resulting in the specific final state of the system (determinism). The probability theory comprises the systems, which are purely stochastic (randomly determined, i.e. not dynamic) or the systems with introduced “noise”.
Phase space represents all possible states of a dynamic system, every of which corresponds to one unique point in the phase space. Poincaré’s works [8] proved that in order to study the progressive evolution of a physical (or biological) system, it is necessary to construct the model based on the laws of physics and list the sufficient and essential parameters characterizing the system (mostly differential equations). In such a way the state of a system can be defined at a given moment. A set of such system states constitute the phase space.
We shall exemplify the above said by a model. In terms of the control theory, the state of a complex dynamic system is construed as the minimal number of state variables to be defined in the initial time t0 in order to predict its future state at any point in time t>t0 within the framework of mathematical description of a system.
Dynamic properties of a system can be described by two equations explaining the states of a system in different points in time [7]. Output signals of a system are defined through the vector of state by means of one more equation. Thus, the first equation is differential, determines the state of a system and sets its dynamic parameters; the second equation determines the output signals of the system depending on its current state. The given vector of the system state is х, the vector of input signal is v, and the vector of output signal - y. Equation of the deterministic system is expressed in the following relations:
x(t) = Ф [x(t), v(t)]; y(t) = × [x(t), v(t)],(1)
in which x means vector length m, y means vector n, v means vector length l.
Systems expressed by linear differential equations:
x = Ax + Bv; y = Cx + Dv
in which matrices А, В, С, D have the sizes (m × m), (m × l), (n × m) and (n × l), respectively. The system expressed by equations (2), is given in Fig. 1.
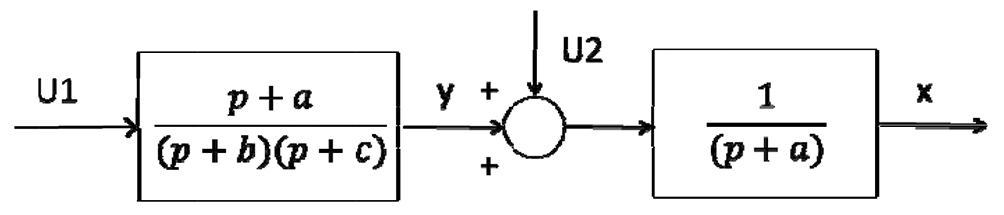
Fig. 1. The diagram illustrating two successively introduced linear equations
The diagram of a system of two linear equations is given in Fig. 2.
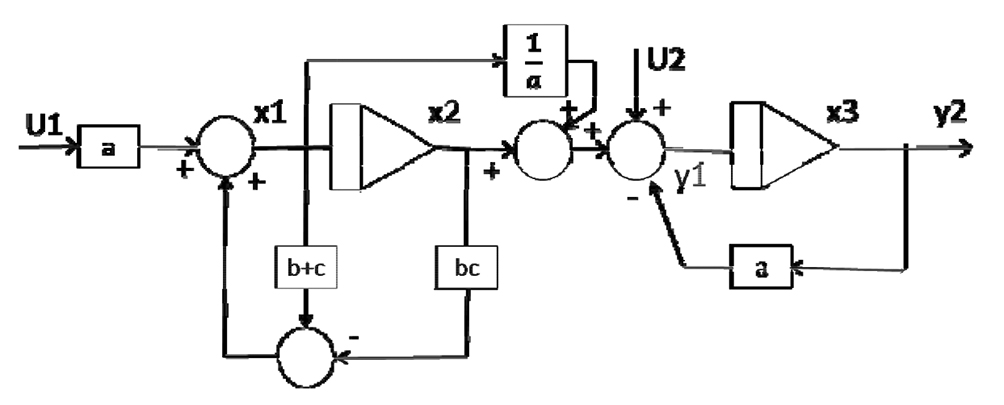
Fig. 2. The diagram of modeling system consisting two linear elements
Equations of the simple system state given in Fig. 1 appear as follows. We shall make a vector of system state from the output signals of integrators in the modeling system. Output signals are defined through х1, х2, х3, from left to right.
Equation is expressed as follows:
x1 = - (b+c)x1 - bcx2 + au1;
x2 = x1;
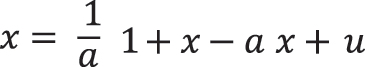
The given model can be used in the experiment for evaluation of the current system state under the impact of physical exercises on the athlete's body. The system is linear if it is equal to the sum of its constituents. Mostly, the systems tend to be nonlinear and are based on the constant balance between strict order and total disorder (chaos). Such phenomena as homeostasis, self-organization and quasi-attractors have its specific nonlinear effects according to the characteristic Lyapunov time. The greatest achievement of Aleksandr Mikhailovich Lyapunov was his theory of relative equilibria for motion of mechanical systems defined by a finite number of parameters. Within mathematics, the theory considers asymptotical stability of solutions for differential equations in which a variable coefficient goes to infinity. The Lyapunov time is the characteristic timescale on which a dynamic system is chaotic; it is the time for the distance between nearby trajectories of the system to increase by ten reflecting the limits of the system predictability [5]. Thus, in a linear system, the sum of causes produces a corresponding sum of effects, which is enough to deduce the behavior of the entire system on the basis of the behavior of a single constituent element and to express the scheme through linear equations. In such cases, in terms of reductionism, small modifications lead to small effects, whereas significant ones – to large effects (for instance, greater preload leads to more intense muscle contraction).
Nonlinear equations comprise discontinuous phenomena, such as explosions, tornados, winning a game of hockey. In general, nonlinear solutions are unique and individual. As compared to regular curves from linear equations, the graphic representation of nonlinear equations show breaks, loops and recursions of all kinds of turbulence. In practice, the use of nonlinear models allows for identification of critical points in the system, at which a transitory change might have a drastic effect (in terms of holism). These observations in context of physics have also been applied in other fields (e.g. exercise physiology) in terms of reductionism, as an object (the human body) is analyzed by studying every of its constituents (organs), while in holism, the whole is more than a sum of its constituents, and therefore cannot be deduced from its parts.
Conclusion. In the modern context, an insight into the reactions in an athlete's body to internal and external stimuli is being gained on the basis of determinism, specifically within the framework of deterministic chaos and nonlinearity of complex dynamic biological systems.
References
- Galiley G. Izbrannye trudy v dvukh tomakh, t. 2. (Selected works in two volumes, Vol. 2) / G. Galiley. – Moscow: Nauka, 1964.– P. 131.
- Dimitriev D.A. Variabel’nost’ serdechnogo ritma i arterial’noe davlenie pri mental’nom stresse (Heart rate variability and blood pressure at mental stress) / D.A. Dimitriev, E.V. Saperova // Rossiyskiy fiziologicheskiy zhurnal n.a. I.M. Sechenov (Russian Journal of Physiology (formerly I.M. Sechenov Physiological Journal). – 2015. – V. 101. – № 1. – P. 98–107.
- Kolmogorov A.N. Teoriya informatsii i teoriya algoritmov (Information theory and theory of algorithms) / A.N. Kolmogorov. – Moscow: Nauka, 1987. – 304 P.
- Laplas P.S. Izlozhenie sistemy mira (Expositiondusystemedumonde) (Presentation of world system (Expositiondusystemedumonde) / P.S. Laplas / Transl. by V.M. Vasil’ev. Prep. by V.M. Vasil’ev, A.A. Mikhaylov. – Leningrad: Nauka, 1982.
- Lyapunov A.M. Sobranie sochineniy (Collected Works) / A.M. Lyapunov.– Moscow: Pub. hse of AS USSR, 1959. – V. 3. – 374 P.
- Malinetskiy G.G. Nelineynaya dinamika i khaos. Osnovnye ponyatiya (Nonlinear dynamics and chaos. Basic concepts) / G.G. Malinetskiy.– Moscow: URSS, 2006. – 237 P.
- Metody matematicheskoy biologii. Kn. 7. Metody analiza i sinteza biologicheskikh sistem upravleniya (Methods of mathematical biology. B. 7. Methods of analysis and synthesis of biological control system). – Kiev: Vishcha shkola, 1983. – 240 P.
- Poincare H. Izbrannye trudy v 3 tomakh, T. 1. (Selected Works in 3 volumes, V. 1) / H. Poincare. – Moscow: Nauka, 1971.
- Haken G. Sinergetika (Synergetics) / G. Haken. – Moscow: Mir, 1980. – 404 P.
- Shannon K.E. Raboty po teorii informatiki i kibernetike (Works on theory of computer science and cybernetics) / K.E. Shannon. – Moscow: Inostrannaya literatura, 1963. – 829 P.
- Chaisson E.J. The Natural Science Underlying Big History // ScientificWorldJournal. 2014: 384912. Published online Jun 17, 2014. doi: 10.1155/2014/384912
- Descartes R. Meditationes de prima philosophia, Quoted: J. Cottingham, R. Stoothoff, D. Murdoch. The Philosophical Writings of Descartes. 3vols. Cambridge, UK: Cambridge University Press, 1988.
- Kepler J. Astronomia Nova. Quoted Donahue WH, Cambridge, UK: Cambridge University Press; 1992.
- Newton, I. PhilosophiaeNaturalis Principia Mathematica. London, 1686.
Corresponding author: apokin_vv@mail.ru
Abstract
The approach to sports science, based on emerging ideas about the reactions of an athlete’s body to internal and external stimuli with regard to the ideas of determinism, stochastics, deterministic chaos and nonlinearity of complex dynamic systems, is being developed.
Nonlinear models in practice can be used to determine the critical points in the system, in which shortterm changes can have severe consequences (from the holistic point of view). The noted observations in physics are applied in other areas of science (e.g., sport physiology) in context of reductionism when a holistic object (human body) can be analyzed by examining each of its constituent elements (organs), while from the holistic viewpoint whole is greater than the sum of its components and, therefore, can not be inferred from its parts.
Today, an idea of reactions in an athlete’s body to internal and external stimuli is being formed, based not only and not so much on the ideas of determinism, but in the framework of deterministic chaos and nonlinearity of complex dynamic biological systems.



