Structural and parametric reorganization of technique of gymnastic exercises
Фотографии:
ˑ:
Professor, Dr.Hab. V.I. Zagrevskiy1
Professor, Dr.Hab. O.I. Zagrevskiy1
1National Research Tomsk State University, Tomsk
Keywords: routine technique, phase structure, motor sequence modelling, programmatic control
Introduction
A solution sequence for the problem of gymnastic motor skill improvement driven by movement structure and parameters control will be designed so as to, first of all, make a preliminary assessment (on a qualitative and quantitative basis) of the contribution of the parametric realignments to the phase structure of the routine to ensure the desired performance and, based on the assessment, outline the ways to excel the individual performance technique of the athlete [3, 4]. We made an attempt to offer a solution for the above problem using a computer model of the sport routine performance techniques [1, 2] with the motor sequences being broken down to the phase elements and the required parameters of the bio-system’s kinematic conditions being preset on the movement phase division lines within the modelled motor sequence.
Objective of the study was to determine regularities in variations of the biomechanical conditions of the subject bio-system on the phase division lines within the routine sequence with the kinematic structure of the control actions being purposefully varied.
Study results and discussion
1. Gymnast's body position variations. Subject to modelling was one of the elements of the gymnastic routine on parallel bars, namely the backward handspring into handstand on bars. The element was performed by I. Cherkasov, International Class Master of Sport. Based on the biomechanical analysis of the motor sequence we fixed a few key control points (1-5) that include the starting and finishing points of the routine plus the routine phase control points marking the phase division lines in the sequence (Figure 1 hereunder).
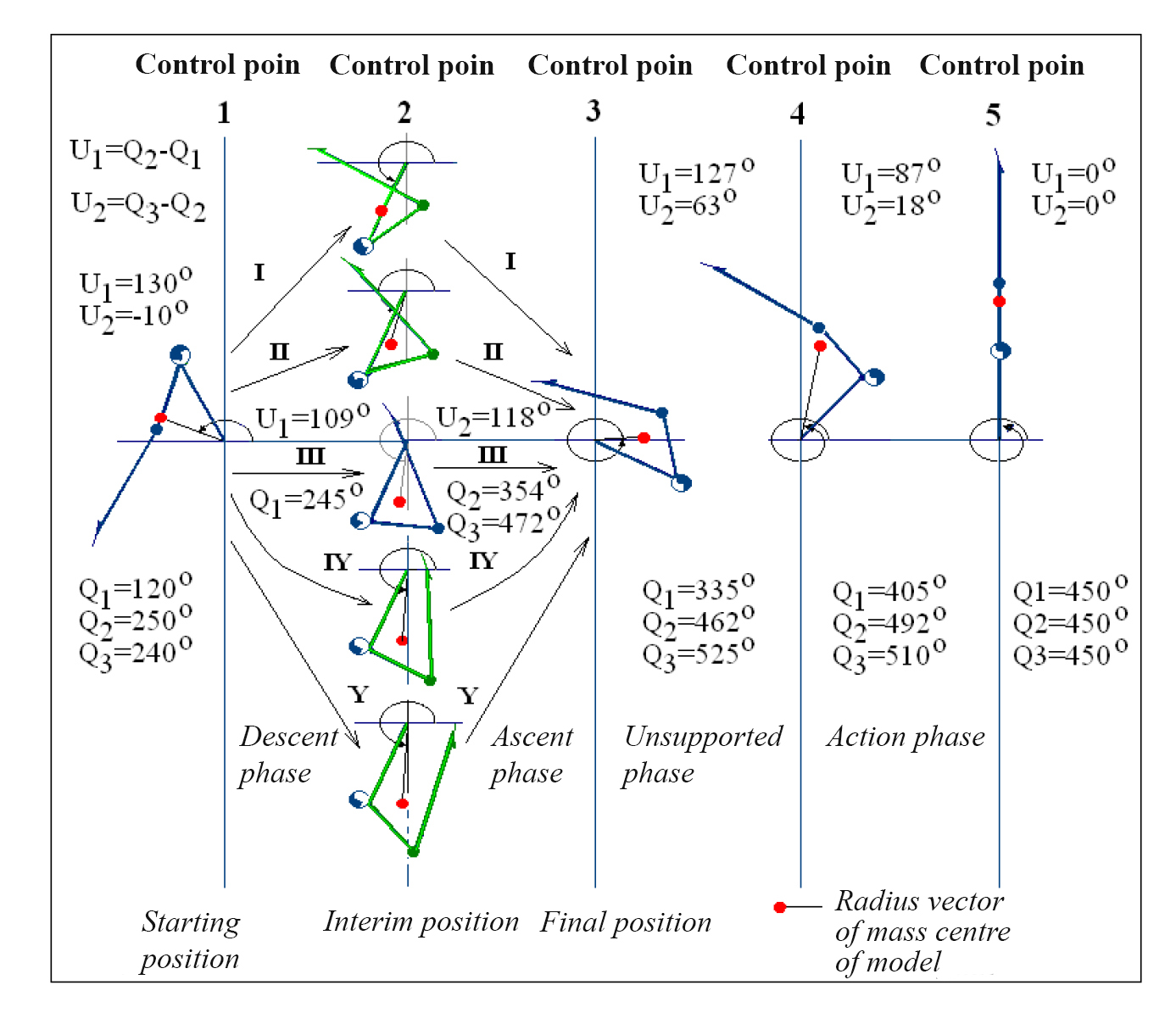
Figure 1. Backward handspring into handstand on parallel bars: biomechanical structure of the routine
The routine started from the gymnast being in the state of rest in the starting position on the parallel bars (control point 1), with every body element having the same angular speed of 0 radian per second (rad/ s) and positioned at the angle of Q1=1200 to axis Ох of the Cartesian coordinate system (generalized coordinates of the arms); Q2=2500 (generalized coordinates of the body); and Q3=2400 (generalized coordinates of the legs). Control point 2 refers to the interim position of the body at the moment when the gymnast comes to the vertical position above the support. Control point 3 refers to the position of the body at the moment when the gymnast’s hands lose contact with the bars. Figure 1 option III shows positions of the body elements at the moment when the hands come in contact with the bars (control point 4) after the free-flight phase of the routine followed in its turn by the handstand on the bars (control point 5) as performed by I. Cherkasov.
2. Parametric adjustments in the programmatic control pattern. Programmatic control for the purposes of the study was presented by the flexion-extension movements in the shoulder joints (U1) and hip joints (U2) calculated as the difference of the generalized coordinates of the model elements as follows: U1=Q2-Q1, U2=Q3-Q2. We assumed under the model that one of the potential options of the parametric realignment of the modelled routine performance technique may be driven by different positions taken by the gymnast in bent hang (control point 2): with the raised (Figure 1, options I-II) or lowered (Figure 1, options IV-V) pelvis positions in relation to the shoulder joints (Figure 1, option III). The legs-to-body angle at the moment of the gymnast’s body passing control point 2 stays the same (680), and the angular variations are limited by only the shoulder joints taking the following values: 310 in option I; 510 in option II, 710 in option III, 910 in option IV and 1110 in option V. Spatial position of the athlete’s body elements is fixed in every other control point. Therefore, in the descent phase the shoulder-joints programmatic control pattern varies in the amplitude and thereby secures the body position being variable in control point 2. The amplitude of the kinematic flexion of the hip joints (1280) in the descent phase under any option (I to V) of the modelled movement stays the same.
3. Path-specific variations of the model elements are given on Figure 2 hereunder: they represent variations of the shoulder-joints programmatic control pattern in the descent and ascent phases as determined by the computing experiment completed in accordance with the recommended procedure [1, 2]. It should be noted in this context that the transition of the biomechanical system from the same starting position (SP) to the same final position (FP) may go through a variety of postures in the interim position (IP). At the same time, regardless of the variability of the shoulder-joints programmatic control pattern under different options (I to IV) of the descent/ ascent movement sequences, the biomechanical system makes a transition from the same spatial SP to the same spatial FP.
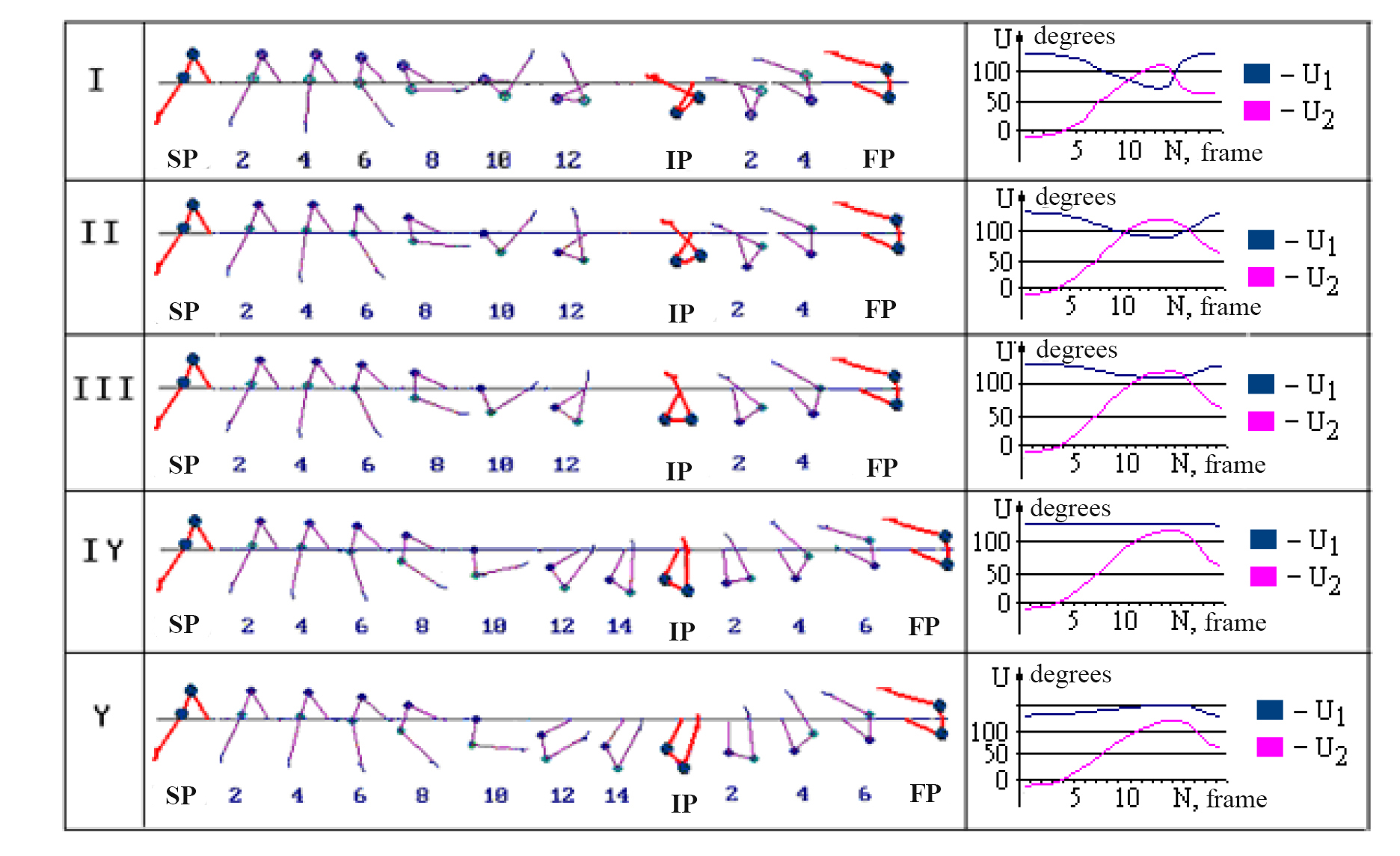
Figure 2. Modelled path options (I to V) of the biomechanical system subject to shoulder-joints (U1) and hip-joints (U2) programmatic control patterns with the body coming to the same final position (FP) from the same starting position (SP) after going through the optional interim positions (IP)
The above mentioned options of the biomechanical system reaching the specified spatial position gives the means to purposefully improve the sport path performance technique with the athlete’s progress being verified by the relevant kinematic/ dynamic performance indicators being attained in the relevant control points on the phase transition/ division lines.
4. Kinematic properties of the biomechanical system in the specified final position are driven by the extremum (maximum or minimum) achievement conditions in the control points of the phase transition under the programmatic control pattern. The transitions from joint flexions to extensions and vice versa in the control points are related to the extreme amplitudes under the programmatic control pattern being attained and, hence, it is the points when the programmatic control speed comes to zero and, as a result, angular speeds of different body elements (arms, trunk, legs) are the same (see Figure 3, А).
Therefore, the simultaneous transition from the flexion movement to extension movement and vice versa in a few joints is associated with the angular speeds of all the body elements being levelled in the zones adjacent to these joints. This is also the reason why the supported flexion action in the joints gives higher angular speed to the distal element versus that of the proximal element of the bio-system.
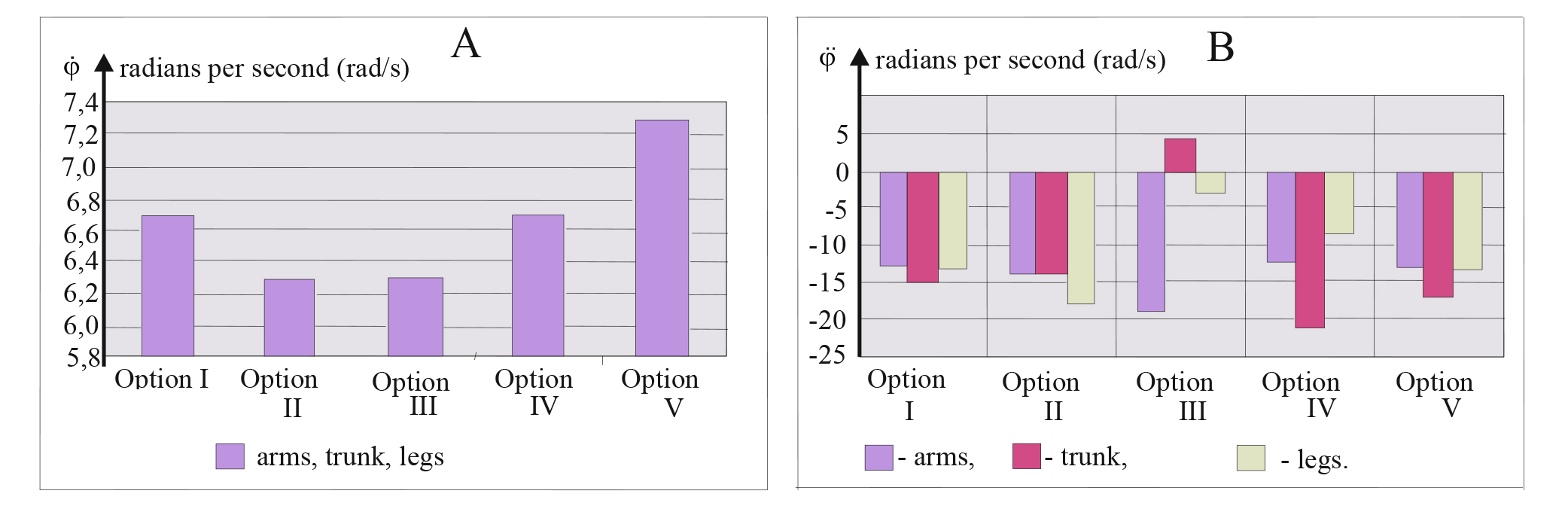
Figure 3. Angular speed (А) and angular acceleration rate (В) of the model elements in the final position, under different movement path options
The regularities detected for the angular speed are found irrelevant for the angular acceleration rates of the model elements (Figure 3, В).
5. Dynamic properties of the biomechanical system in the specified final position are driven by the differences in variations of the space-and-time-specific indicators of the model elements; and this is demonstrated by the control moments of muscular forces in the model joints (Figure 4).
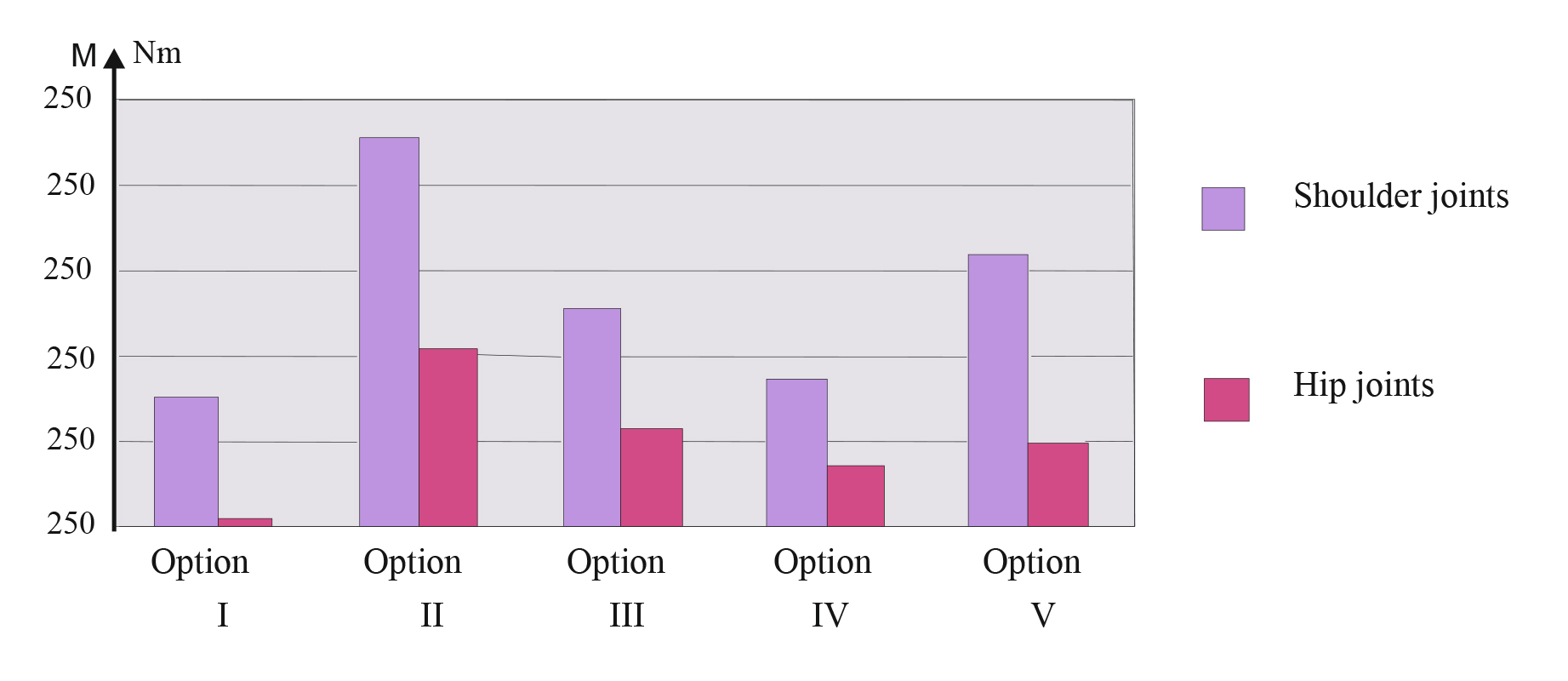
Figure 4. Control moments of the muscular forces in the model joints, for the final position (FP) under different model movement path options
Since the dynamic characteristics are the function of the angular speeds and angular acceleration rates, every change to the space-and-time-specific indicators of the model elements force the relevant changes to the parameters of dynamic characteristics under every option of the model movement sequence.
Conclusions
- The structural-and-parametric realignment of the gymnastic routine performance technique is based on the programmatic control pattern variations in the specific phases of the movement sequence at the kinematic level that means the variations in amplitudes and durations of the flexion-extension movements of the athlete’s joints.
- The forecast outcomes of the structural-and-parametric realignment of the gymnastic routine performance technique are obtainable through a computing experiment using the computerized movement sequence simulation tool acting within the preset/ required kinematic state in the interim positions.
- Transition of the biomechanical system from the specified starting position to the required kinematic state (as identified by the spatial characteristics) may go along different path options of the bio-system elements.
- Under the same bio-system condition (as specified by the spatial characteristics) in the final position, the space-and-time-specific indicators and dynamic characteristics of the routine performance may be the same (although measurable by different parameters).
References
- Zagrevskiy, V.I. Komp’yuterny sintez dvigatel’nykh deystviy s upravleniem dvizheniem po kinematicheskomu sostoyaniyu biomekhanicheskoy sistemy (Computer synthesis of motor actions with movement control based on kinematic condition of biomechanical system) / V.I. Zagrevskiy, O.I. Zagrevskiy // Teoriya i praktika fizicheskoy kultury. – 2013. – № 7. – P. 10–15.
- Zagrevskiy, V.I. Komp’yuterny sintez tekhniki sportivnykh uprazhneniy na osnove upravleniya konechnym sostoyaniem biomekhanicheskikh sistem (Computer synthesis of exercise technique based on control of final state of biomechanical systems) / V. Zagrevskiy // Teoriya i metodika fizicheskogo vospitaniya i sporta. – 2014. – № 1. – P. 70–75.
- Kapilevich, L.V. Fiziologicheskie mekhanizmy koordinatsii dvizheniy v bezopornom polozhenii u sportsmenov (Physiological mechanisms of unsupported movement coordination in athletes) / L.V. Kapilevich // Teoriya i praktika fizicheskoy kultury. – 2012. – № 7. – P. 45–48.
- Koshel’skaya, E.V. Fiziologicheskie i biomekhanicheskie kharakteristiki tekhniki udarnotselevykh deystviy futbolistov (Physiological and biomechanical characteristics of football shooting technique) / E.V. Koshel’skaya, L.V. Kapilevich, V.N. Bazhenov et al. // Byulleten’ eksperimental’noy biologii i meditsiny (Bulletin of experimental biology and medicine). – 2012. – V. 153. – № 2. – P. 235–237.
Corresponding author: o.zagrevsky@yandex.ru



