PhD V.N. Pritykin^1
1Omsk State Medical University, Omsk

Keywords: basketball, technique, backboard-free shot, ball trajectory parameters, target specifications, accuracy, computer software, teaching aids

Introduction

It is a matter of common knowledge that a throw performance technique is to be a top priority in a basketball training system to help players master and improve their shooting skills [3, 4, 7, 9, 10, 11], with special emphasis being made on the ball trajectory that is determined by the individual follow-through technique specific for every athlete [1, 2, 12]. Necessary knowledge on this topic may be obtained from the available calculations and theoretical analysis of the basketball throw parameters versus the target specifications [5]. It was in 1996 that a theoretical study report was published giving the correlation analysis of the sizes and shapes of the basketball targets versus the relevant ball follow-through movement parameters [6]. Further studies provided more important data to: clarify and define more precisely the qualitative and quantitative indicators of the above correlations; develop the application computer software “Backboard-free basketball shot trajectory calculations (Basket)” [8]; and design the relevant teaching aids to help players master the backboard-free shooting techniques.

Objective of the study was to analyze the ball trajectory parameters of the backboard-free shooting techniques in correlation with the relevant variable specifications of the targets.

Methodology and organisation of the study

Definition of a basketball target

Shot accuracy (or target hitting probability) in case of a ballistic projectile (stone, arrow, ball etc.) flying to the target basically depends on the target size and shot distance.

The following mathematical formula was offered as a tool for optimization of the basketball throw trajectory [6]:

Ω = F sin α / L2,                          

where F means the square of the target within the hoop plane (see Figure 1) that guarantees the ball flying through the basket conditional on its centre hitting any point of this target; α means the angle formed by the ball trajectory crossing the hoop plane; L means the length of the ball trajectory from the hand to the centre of square F; Ω means the target function (or angular size of the target) that is critical for the shot accuracy.

If we now analyze the above formula, we will find that the lower is the target angle α, the lower is the Ω value that may go down to negligibly small figures. On the other hand, Ω values are also low when α angle is too high due to high L distance. This means that there is some range of maximum Ω values specific for the optimal ball throw trajectory.

Mathematical calculations of the above parameters were made with due consideration for the thermodynamic properties of the ball travel medium, spin on the ball and rebound of the ball from the rim of the hoop [5]. Subject to the calculations were the backboard-free shots from distances of 3 to 7.5 meters. In modern basketball game, most of these shots are performed as one-hand overhead set-shots (in standing positions typically used for free throws) and jump-shots.

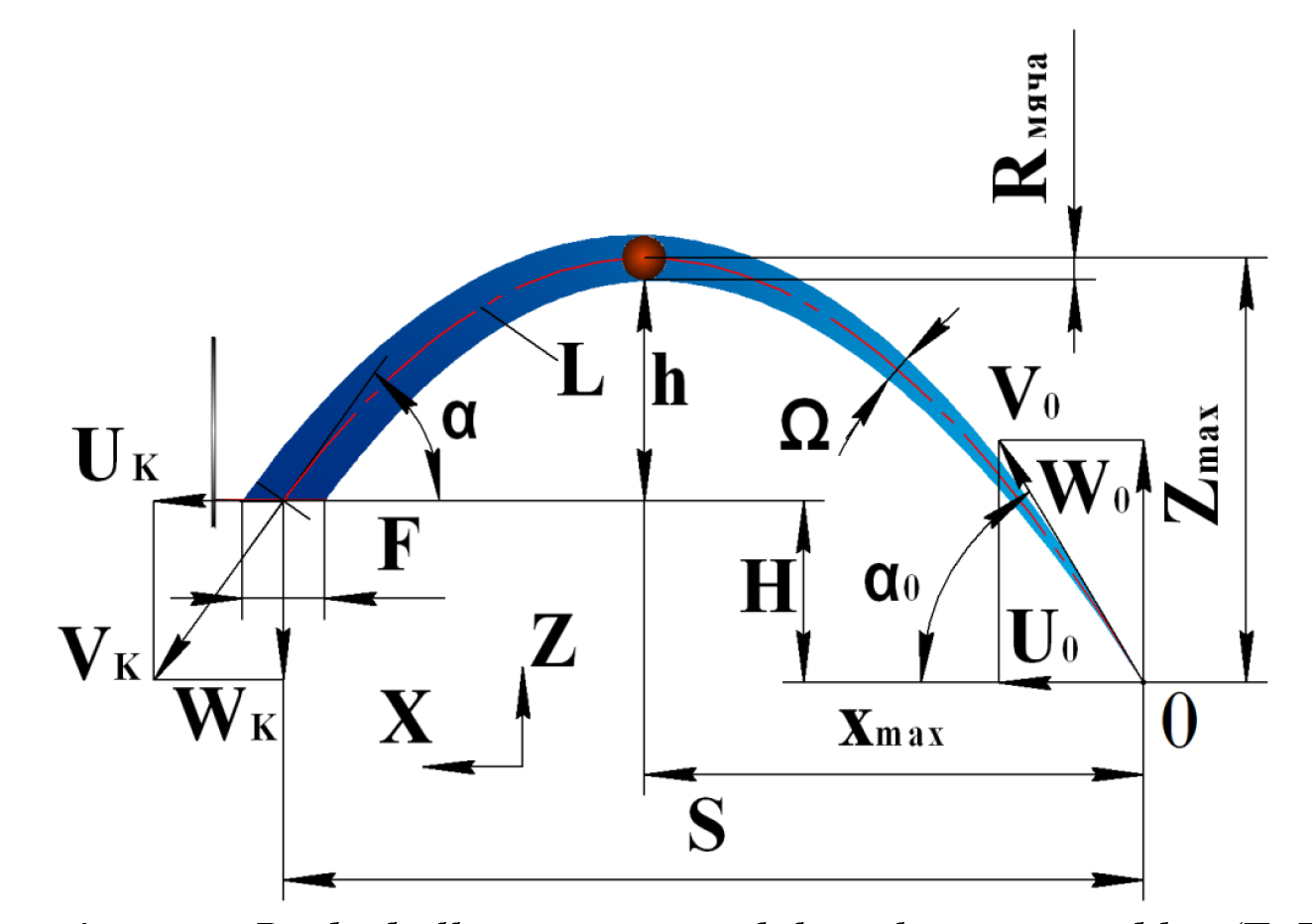
Figure 1. Basketball target size and the relevant variables (F, L and Ω values are provisional)

R- radius of the ball

Contour of the target (that is the cross-section of the multitude of the ball-centre trajectories by the hoop plane, with the trajectories guaranteeing the ball falling through the hoop with acceptable contacts with the rim provided they have no effect on its route) let us call herein the clear target. Figure 2.2 hereunder shows the clear target (F_с) that may be described as a circle made by the centre of the ball rolling inside the hoop, with the maximum square of the clear target being equal to 20% of the hoop square. Centre of the clear target is always in the geometric centre of the hoop. Normally the ball comes to the hoop plane at an acute angle that means that the hittable target is even smaller in this case. The target is generally oval-shaped and may vary from sharp-pointed to sub-circular (or elliptical) shape. Ball hitting the target may fall through the basket either cleanly or with some rebound from the rim.

The target contour line – that means the borderline between the successful and non-successful ball contacts with the rim of the hoop – we would call herein the broad target or real target. Centre of the broad target do not coincide with the geometric centre of the ring as it is somewhat shifted to the far rim due to the asymmetric contribution of the near rim versus the far rim of the hoop in a variety of contacts with the ball [5].

Having specified the key parameters of the basketball target and ball trajectory (L, α and F), one can calculate and analyze the target function Ω using the above formula (1) to obtain parameters of the optimal trajectory that secures the Ω values coming to the maximum.

Based on the calculations and theoretical analysis of the varieties of basketball shot trajectories and effective target geometry, the research team of the Physical Culture and Sport Research and Practice Study Laboratory “Perspektiva” has developed the earlier mentioned application computer software “Backboard-free basketball shot trajectory calculations (Basket)” [8].

Study results and discussion

Hittable target parameters depending on the ball trajectory factors

Figure 2.1 hereunder shows the typical ball trajectories including, for instance, the lowest Trajectory 1 when the ball can fall through the basket only with rebound off the far rim with the attack angle α₀ being equal to 39º. Figure 2.6 presents the evolution of the broad target with the attack angle α₀ varying from 39º to 48º. When α₀ = 39º, the broad target emerges on the far rim of the hoop as a small sharp-pointed oval spot (see Figure 2.3). With the growing attack angle α_0, the broad target rapidly grows taking oval shape with its far edge being virtually immovable whilst the near edge moves towards the near rim and, when it comes to the ring centre and passes it at α₀=48°, it transforms to the clear target having a sharp-pointed transverse oval shape much similar to the broad target shape.

Figures 2.4 and 2.5 hereunder show further evolution of the target with further growth of the attack angle α₀. The clear target also takes oval shape with the growing attack angle, but it stays always centred and symmetrical in relation to the geometric centre of the ring. It is worth noting in this context that the squares of both the clear target and broad target are much smaller than the actual square of the ring as they amount, for instance, to 14% and 28% at the attack angles of α=54º and α₀=60º, respectively.

Broad target components

The broad target that factors in, as mentioned above, the variety of successful ball contacts with the rim, is notably larger (in square and spatial angle) than the clear target by the factor of 2 and more (see Figure 2.4 and 2.5). It is the far rim of the hoop that makes the major contribution to the target broadening effect that is due to the asymmetry of contributions of the near and far rims versus the attack angles of the ball trajectory coming to the ring. The far rim contribution in case of the optimal trajectory, for instance (at α₀=60º), in terms of the target exposure angle, is 4 times higher than that of the near rim (see Figure 2.5) and 13 higher in case of the trajectory of the least-effort throw (at α₀=51º, see Figure 2.4). Our practical education process surveys have confirmed this conclusion on the whole, with the similar relation estimated at 1.7÷7.1. Calculated squares of the clear target and broad target please find hereunder on Figure 3.

Optimal range of the ball trajectories

Optimal trajectories to secure the target exposure to the maximum (Ω_mах) possible degree with the minimum energy demand (Е_min) for the shot may be significantly different, with the extreme ball release angles in the point of S= 4.225 m and Н = 1 m making up α_Ω=60º and α_Е=51º (Figure 4). For the free throws, however, it is the α_Ω that shall be ranked a key index since it determines the trajectory corresponding to the maximum angular size of the target Ω that claims minimum addition of energy (of only 3.7÷7%) to the optimal shot energy demand value at α_Е that is negligible for the mid-distance shots. Qualitative estimates of the achievable shooting accuracy, conditional on every shot being accurately centred, show rise of the shot success rates – for instance, from 73% at the ball release angle of α₀=51º to as much as 82% at the ball release angle of α₀=60º.  It should be emphasized that there is always an optimal ball release angle corresponding to every ball release height point (that basically depends on the body height of the players). The higher the ball release points are (3.05 – Н) the lower the ball release angles α_Ω and α_Е are. The optimal angles α₀ for the reasonable range of the ball release heights (3.05 – 2.05 m) vary from α_Е =44÷51º to α_Ω= 52÷60º. It should be noted in this context that recommendations of the relevant previous study [1] on the best angles α_Ω are found to be in good correspondence with the optimal range we have found herein. However, the above study makes no consideration for the effects of the ball release heights (Н) on the shooting accuracies.

Geometry of the target for the Ω_max-determined optimal trajectories

It is the ring attack angle α =54º that stays constant and irrespective of the ball release point coordinates (S, Н) for a variety of the Ω_max-determined optimal trajectories of the shot. Consequently, geometry of the target within the hoop plane (that may be referred to as the optimal target) is also constant. These notions are illustrated by Figure 2.5 hereunder that presents the variety of the Ω_max-determined optimal trajectories of the shot. The degree of the expanded target being shifted to the far rim is estimated at 3.5 cm. Let us call the above attack angle and the target centre shift the Ω_max: α_opt, х_eopt-determined optimal values. It should be noted in this context that the ratios of squares that comprise the optimal target are integer-valued; that means that the far-rim-rebound-due target expansion increment to the near-rim-rebound-due target expansion increment ratio makes up 4:1; whilst the ratio of the total contribution of the both rims to the target expansion effect to the clear target square makes up 1:1.

Dependence of the expanded target centre shift х_s on the ball release angle α_о and height Н; and the aim control by the shooting player

As mentioned above, the asymmetry of the near-rim to the far-rim contributions to the ball rebounds is the reason for the expanded target centre being shifted towards the far rim from the centre of the hoop. Figure 5 hereunder gives the diagram of how this shift х_s depends on the angle α₀ and height Н for the shooting point S= 4.225 m. Maximum shifts of the target centres are the same for the variety of Н values, being estimated at |х_s|=15 cm. Upper extremes of the х_s (α₀) curves on Figure 5 are not continued upwards, and all the extreme points at the level of |х_s|=15 cm correspond to the minimum acceptable ball release angles α₀ that allow the ball falling through the ring (that means the expanded target emergence or visibility angles). These angles fall within the range of α_0min= 19÷39º that basically means that a tall player may successfully hit the ring at relatively low ball release angles, whilst the shorter players are more limited in the range of release angles.

One more group of the same expanded target centre shifts of |х_с|=3.5 cm is made up by the variety of Ω_max-determined ball release angles of α₀= 51÷60º. Figure 5 presents them as projections of the cross points where the horizontal line |х_с|=3.5 cm crosses the х_с(α₀) curves, on the α₀ axis. Our estimates of the accuracies of shots to the expanded target with aiming at the ring centre m_x = m_y= 0 versus those aimed at the expanded target centre showed that the expanded target centre aimed shots were up to 5% more accurate at σ_х = σ_у, S=4.225 m, and Н= 1 m, and α₀= 60º. For the lower trajectories, the growth of the shooting accuracy is even higher. This finding gives the reasons to make the following practical conclusion: shots shall be made so as to direct the ball trajectory towards the far rim of the hoop, whilst the ball contact with the near rim shall be considered a shooting error – as opposed to the widely popular opinion that it is the near rim that should serve a reference point in the ball aiming process [4]. As far as the methodological aspects are concerned, successful shots with rebounds from the far rim shall be rated as high as the “clean” shots.

Our analysis of the available educational data shows that basketball players tend to see no difference in rebounds from the near and far rims. In terms of the free throw performance statistics, the ratio of the far-rim-rebounded shots to the near-rim-rebounded shots varied from 0.6 to 2.1 and averaged 1.2.

Conclusions

1. The mathematical model developed and offered hereby is reliable enough in assessing the ball trajectories with account of the actual environmental conditions, spins on the ball and the ball rebounds from the rim of the hoop.
2. The qualitative analysis we completed demonstrates that every individual trajectory corresponds to a certain hittable target within the basket ring that is specific in its parameters and geometry and may be characterized by three key constituents. The target is always oval-shaped, the oval form varying from sharp-pointed to sub-circular (or elliptical). Shots from distances of 3 to 7.5 meters shall be duly aimed to bring the shot success probability rate to the maximum, i.e. the ball descent (attack) angle shall equal 54º and the hittable target centre shall be shifted towards the far rim of the hoop by 15% from the geometric centre of the hoop, with the hittable target square being 3.5 times smaller than the square of the hoop.
3. The study has found the variety of best trajectories that secure the maximal target exposure (Ω_max) with the minimum energy demand (Е_min) for the shot, the variety being called herein the range of optimal trajectories. Furthermore, we specified the extremes of the range of optimal trajectories: for instance, the ball release angles of the free throws may vary within 15%, whilst the ball release speeds are 3% different; and the hittable target square is reduced by 23% when the shot energy demand is minimized.
4. To ensure the basketball throw being always successful and reliable, the athletes and coaches are recommended to implement in the training systems and practices the backboard-free-throw aiming and spatial orientation method based on the following key principles:

• It is the centre of the far rim of the basket hoop that shall always be a point to aim the throw at;
• Ball contacts with the near rim of the hoop shall be avoided;
• Maximal height of the ball trajectory shall never be higher than the upper edge of the backboard;
• Proportion of the successful shot with rebounds from the near rim and far rim shall be kept within 1:7, respectively; and
• Counts of misses after the ball rebounds from the near and far rim shall be about the same.

For the training practices to improve the shot accuracy rates being consistent and successful, coaches shall ensure the relevant instruction manuals and teaching aids being always available for the teams to help upgrade the relevant knowledge and skills of the basketball players. As a case in point we attach hereunder the sample poster “Range of optimal backboard-free shot trajectories for free throws” (Figure 2).

Figure 2. Range of optimal backboard-free shot trajectories for free throws

Shot accuracy criterion: Ω = F sin α / L2      

where F means the square of the target within the hoop plane that guarantees the ball flying through the basket conditional on its centre hitting any point of this target; α means the angle formed by the ball trajectory crossing the hoop plane; L means the length of the ball trajectory from the hand to the centre of square F; Ω means the target function (or angular size of the target) that is critical for the shot accuracy.

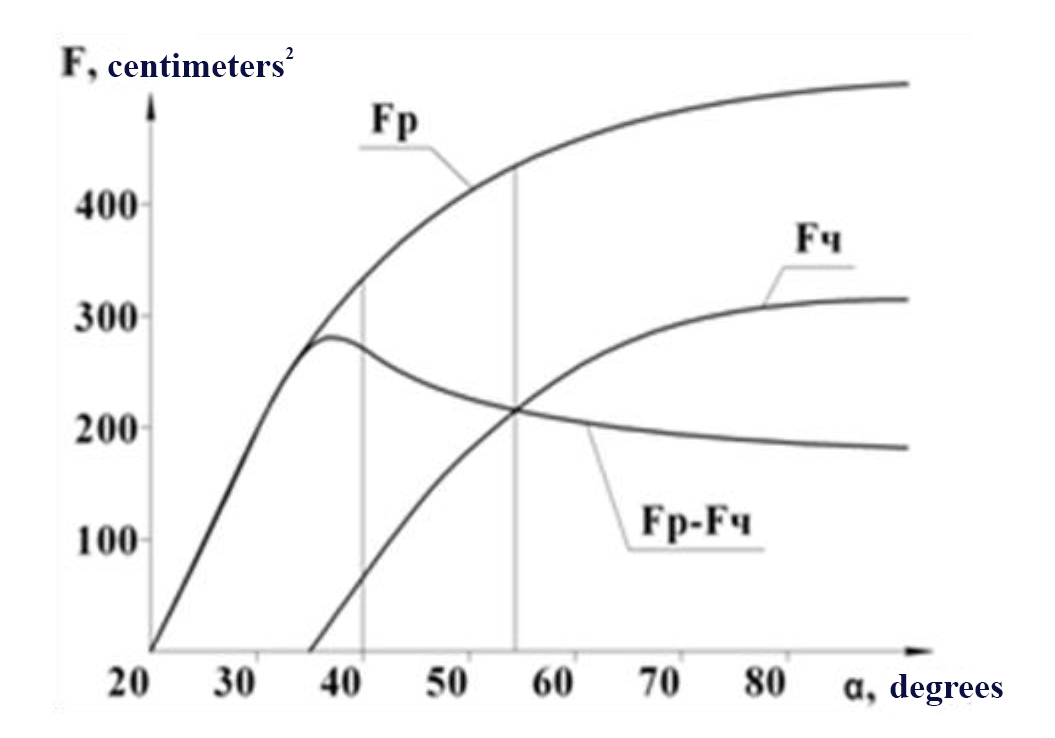
Figure 3.3 Squares of the broad target Fb, clear target Fc and target expansion increment (Fb – Fc in cm2) (due to the ball rebound from the rim) versus the ball attack angle α

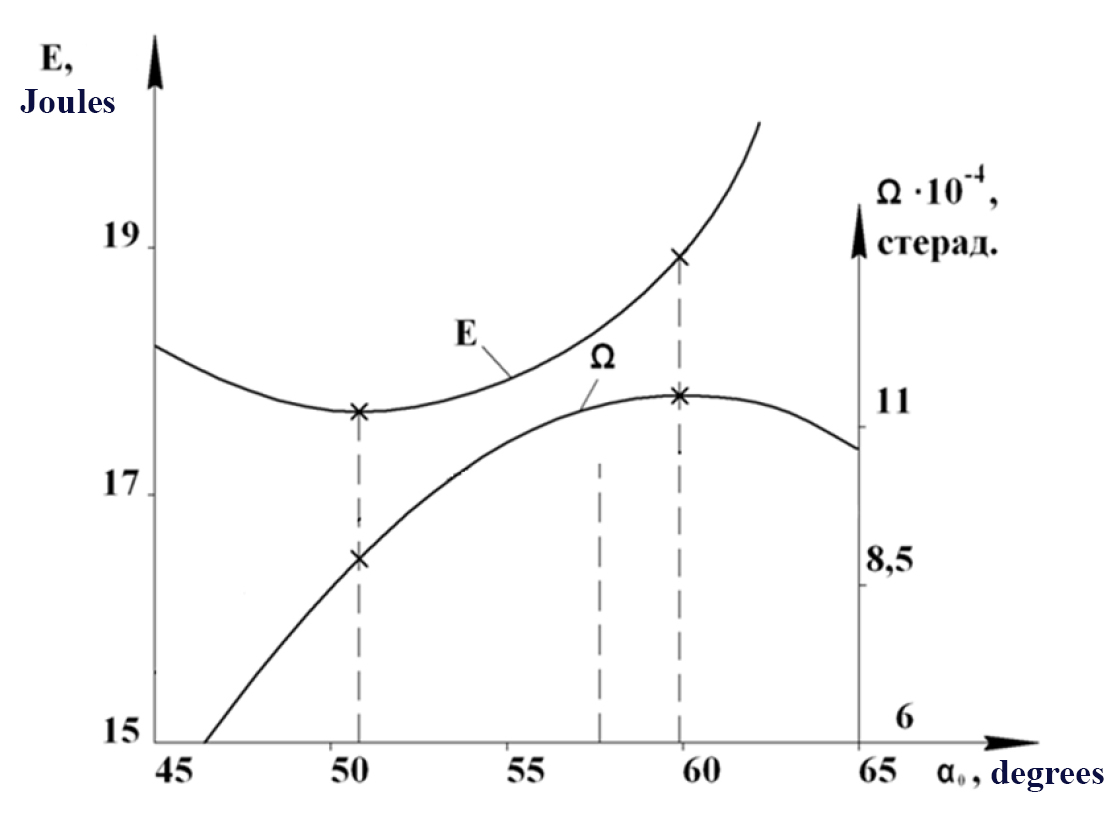
Figure 4.3 Target spatial angle Ω and shot energy demand Е (joules) versus the ball release angle α0 for the shooting point S = 4.225 m, Н = 1 m

Summary:

1. Success rate of the far-rim-rebounded shots is 2-7 higher than that for the near-rim-rebounded shots;

2. Ball contact with the near rim shall be considered an error.

3. Recommended optimal trajectory range falls within trajectories II and III.

References

1. Golomazov S.V. Issledovanie mekhanizmov upravleniya tochnost’yu dvizheniy i eksperimental’noe obosnovanie metodiki ee povysheniya: avtoref. dis. … kand. ped. nauk (Study of motion precision control mechanisms and experimental substantiation of methods of its improvement: abstract of PhD thesis 13.00.04) / S.V. Golomazov. – Moscow, 1973. – 30  P.
2. Cousy B. Basketbol: kontseptsii i analiz (Basketball: concepts and analysis) / B. Cousy, F. Power; trans. from English by E.R. Yakhontov. – Moscow, 1975. – 272 P.
3. Krauze Jerry В. Basketbol – navyki i uprazhneniya (Basketball skills and drills) / Jerry В. Krause, Don Meyer, Jerry Meyer; transl. from English.– Moscow: AST: Astrel’, 2006. – 211P.: il. 
4. Nesterovsky D.I. Basketbol. Teoriya i metodika obucheniya: uchebnik (Basketball. Theory and methodology of training: textbook) / D.I. Nesterovsky, 4th ed. – Moscow: Academia, 2008. – 336 P.
5. Pritykin V.N. Netraditsionnye podkhody k povysheniyu tochnosti shtrafnogo broska v basketbole: monografiya (Innovative approaches to improve basketball free throw accuracy: abstract of PhD thesis 13.00.04) / V.N. Pritykin. – Omsk: OSMU Pub. h­se, 2015. – 175 P.
6. Pritykin V.N. Opredelenie optimal’nykh traektoriy poleta myacha i kharakteristik tseli v basketbole pri broskakh po kol’tsu so srednikh i dal’nikh distantsiy (Determination of ball flight optimal trajectories and target characteristics in basketball in throws from middle and far distances) / V.N. Pritykin et al. // Teoriya i praktika fizicheskoy kultury. – 1996. – № 10. – P. 48–54.
7. Pritykin V.N. Organizatsionnaya struktura kompleksnykh metodik tekhniko­takticheskoy podgotovki v basketbole (Organizational structure of integrated technical and tactical training technologies in basketball) / V.N. Pritykin, N.S. Morozova, S.V. Sukharev // Teoriya i praktika fizicheskoy kultury. – 2009. – № 2. – P. 38–41.
8. Pritykin V.N. Raschet parametrov basketbol’nykh broskov bez otrazheniya myacha ot shchita («Basket»): svidetel’stvo o gosudarstvennoy registratsii programmy dlya EVM # 2014611231 (Backboard-free basketball shot trajectory calculations (Basket)”: certificate of state registration of the computer program № 2014611231) / Pritykin V.N., Petrushov I.V., Bokov I.S., Kuznetsova N.S. (Russia) – № 2014611231; decl. 03.12.13; pub. 28.01.14.
9. Sourtel N. Basketbol: 100 uprazhneniy i sovetov dlya yunykh igrokov (Basketball: 100 exercises and tips for young players) / N. Sourtel, transl. from English. – Moscow: AST: Astrel, 2002. – 240 P.: il.– (First steps in sport).
10. Yuny basketbolist: posobie dlya trenerov (Young basketball player: trainer's manual) / ed. by E.R. Yakhontov. – Moscow, 1987. – 172 P.: il.
11. Filippi A. Shoot Like the Pros: The Road to a Successful Shooting Technique / Adam Filippi. – Chicago, Illinois: Triumph Books, 2011. – 164 P.
12. Kudimov V.M. Formuvannya ta udoskonalennya navichki shtrafnogo kidka u basketbolI z vikoristannyam tekhnichnikh zasobIv (Formation and improvement of basketball free throw skill using different techniques) / V.M. Kudimov, abstract of PhD thesis – 24.00.01 – Olympic and professional sport // Kharkiv State Academy of Physical Culture. – Kharkiv: KhSAPC. – 2006. 17 P.

Corresponding author: osma_fk@mail.ru