Efficiency of Golf Training as a Transfer Function of Quasistationary Spectra of Performance
Фотографии:
ˑ:
A.N. Korol'kov, associate professor, Ph.D.
Russian state university of physical culture, sport, youth and tourism (SCOLIPC), Moscow
Key words: golf, spectral analysis, performance, efficiency of training.
Introduction. In any sport results can be presented as time functions: numerous discrete values of instants and relevant results. The duration of time intervals where sports results are fixed can vary: from time of a single training class, time of a training micro- or mesocycle to duration of sports career.
The analysis of time changes of the results in sport and of various tests usually serves a measure of efficiency of athlete’s training. Various quantitative indices are used as a measure of efficiency, ultimately coming to the calculation of the ratio of the pre-exercise and post-exercise results. These relations are an analogue of the gain coefficient, transmission factor, performance factor etc. in different branches of science and technology. Such assessments are common when estimating efficiency of actions of social institutions. For example, performance of the Ministry of Internal Affairs is estimated by the ratio of the number of committed crimes and the total of registered ones.
Pareto efficiency is frequently used when analyzing socio-economic systems, which is determined as a system state where the value of each particular indicator characterizing the system cannot be improved without degradation of others [5].
The purpose of the study was to describe the method of presenting the relationships of changes in sports results in golf and time in the form of amplitude-frequency distribution.
Results and discussion. The efficiency indices, determined as a ratio of pre-exercise and post-exercise results of tests or competitions are generally used in the theory and practice of sport [1-3]. Such efficiency indices, frequently called “integral”, characterize changes that have happened in the state of athletes in general, but they are not enough to judge by the structural changes in states.
In the meantime, if to imagine the time series of results in the form of harmonious series, one can determine the amplitude-frequency and phase-frequency distributions of performance, compare these distributions with the ones defined in other timing cycles of sports training, define the frequencies where the most significant changes take place in athletes’ results, and calculate the efficiency of training effects in the form of transfer functions. These data can be used after to correct training and competitive activities.
The educational experiment with 9 golf players aged 14-16, qualified from the grade II to candidate for master of sports was held to confirm the hypothesis. At the beginning of the special pre-season all the players were striking the same hole for mini golf for an hour fixing the number of hits in scorecards. A similar test for the same players was made a month later at the end of the pre-season. The transformations of time series of obtained results by Fourier resulted in the calculations of the amplitude-frequency distribution of athletes’ performance. Their examples are adduced on Fig. 1.
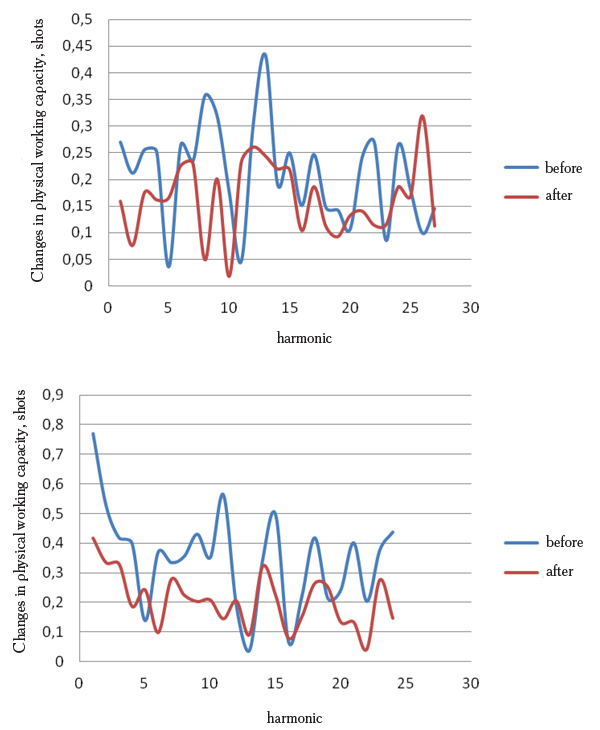
Fig. 1. The amplitude-frequency distribution of performance of two athletes before and after the special pre-season
Proceeding from the findings, the amplitude-frequency distributions for every athlete are similar to each other and highly coherent (0,864006 and 0,92692): rates of increase and decrease of performance are quasistationary in time and their changes show the training effect.
Performance improved in both cases – the performance variance reduced but the alternating frequencies in the results remained. The distribution minimums correspond to the time frequencies of maximum performance, while the maximums indicate to deterioration of results. The first athlete had substantial gaps in the game in the 4, 7, 9 and 14th harmonic series, i.e. with the frequency 15; 8,6; 6,7 and 4,3 min-1; while the second athlete – in the 12, 15, 18 and 22nd harmonic series respectively. The peak performance increments seem to match by the range the ultradian rhythms of cerebrospinal fluid oscillations, its prolonged congestions [4].
Fig. 2 shows the transfer functions of performance, calculated as a ratio of pre- and post-exercise amplitude-frequency distribution (Fig.1.). The transfer functions are obviously significantly different and individual for different athletes: performance changes at various frequencies. The transfer function is supposed to be a specific individual image of a subject quasistaionary in time that can be compared with other cycles, which determine, for example changes in attention focusing, long-period processes of central excitatory and inhibitory states. This assumption needs additional checking.
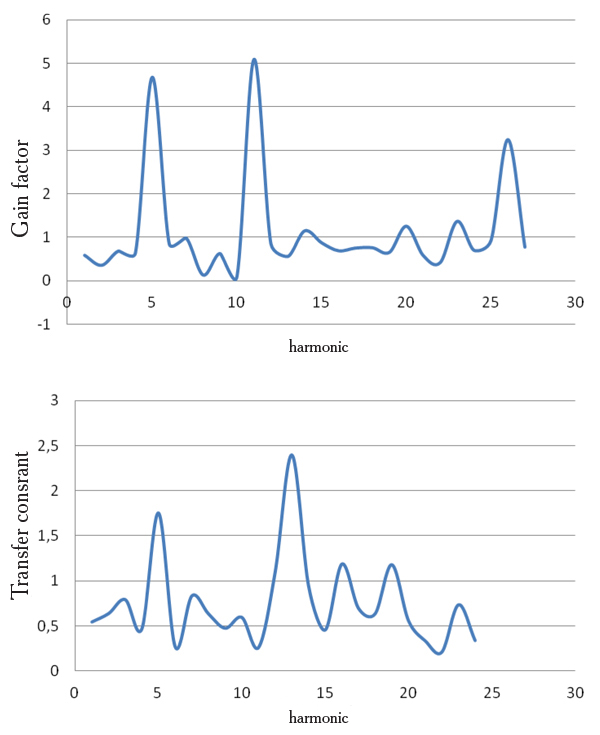
Fig. 2. Transfer functions of performance for two athletes (transfer constants of performance by frequency)
Conclusions. The findings are of great educational value in golf for determining individual tactical playbooks in respect to allocating the duration of playing intervals at temporal frequencies concurring with the peaks of deterioration of efficiency, which can be filled with imitations of playing actions or their ideomotor performance. The analysis of the amplitude-frequency distribution provides for allocation of the individual duration of the warm-up before a game and the optimum pace of the game (if it does not contradict the rules of competitions).
References
- Korol’kov A.N. The rules of formation of motor skill in young mini-golf players / A.N. Korol’kov // Fizicheskaya kultura:vospitanie, obrazovanie, trenirovka. – 2011. – № 6. – P. 36–37. (In Russian)
- Korol’kov A.N. On efficiency of extended-constructive method of teaching how to play golf / A.N. Korol’kov, D.S. Titenin // Teoriya i praktika fizicheskoy kultury. – 2012. – № 6. – P. 8. (In Russian)
- Laboratory testing methods for cerebrospinal fluid / Moscow regional scientific-research clinical institute n.a. M.F. Vladimirsky. – Moscow, 2008. – 64 P. (In Russian)
- Nogin, V.D. Decision making in multicriteria environment: a quantitative approach / V.D. Nogin. – Moscow: Fizmatlit, 2002, 2005. – 176 P. (In Russian)
Author’s contacts: korolkov07@list.ru




 Журнал "THEORY AND PRACTICE
Журнал "THEORY AND PRACTICE