Associate Professor, PhD A.V. Tsyganov¹
Dr.Sc.Phys.Math., Professor Y.V. Tsyganova²
Associate Professor, PhD I.V. Stolyarova^1
1Ulyanovsk State University of Education, Ulyanovsk
²Ulyanovsk State University, Ulyanovsk

Keywords: thermometry, thermal homeostasis, discrete linear stochastic system, optimal discrete filtering, MATLAB.

Background. Homeostasis is defined by the modern science as the body’s ability to maintain balanced and efficient functionality of one or another own system (thermal control one, for instance) under aggressive external pressures/ stressors [2]. Presently the human biological circadian rhythms are viewed as the universal functionality criteria indicative of the individual adaptation to the environmental conditions [6].

Any complex problem in some system may be addressed, among other ways, by an adequate mathematical model description and design. Thus the available experimental data on the daily bodily temperature variations may be represented as a mix of the relevant deterministic and stochastic constituents [5], with the deterministic constituent covering the periodical (oscillatory) processes. In the first approximation it may be modeled by a harmonic oscillator with the generally unspecific amplitude and specific (24-hour) time period. And the stochastic constituent of the frame model may be represented as the first-order Gaussian-Markov process with two parameters [diffusion and correlation range (drift ratio)] – that may also be unspecific and subject to identification.

A few study reports [7, 1, 2, 8] have offered the third- and forth-order daily thermometric mathematical models classifiable with the uninterrupted discrete linear stochastic systems (LSS) in the relevant state spaces. The third-order models assume that the daily average temperature (mesor) is known and preset as a positive material constant value; whilst the fourth-order models assume that the daily average is unknown and is included in the state vector among the other values estimated by the filtration algorithm.

Objective of the study was to revise the existing mathematical computer models of daily thermal homeostasis in healthy individuals; and offer a new mathematical model with the discrete linear stochastic systems addressing the state space with unknown inputs and noisy measurements.

Methods and design of the study. Let us assume that the body temperature (^оС) is metered by a thermometer tablet with 5min time intervals for 24 hours – that amount to 280 readings per day on the whole; with the error rate considered a Gaussian occidental value. Let us consider now the following third-order discrete linear stochastic model [6]:

Whereas  means the discretization interval (5min in the case); , ;  means the discrete white noise with zero mathematical expectation and co-variation ; input , ; ; and  means the reading error rate with the zero mathematical expectation and co-variation  (with assumed ). Let’s now set parameters  and  [6].

In contrast to the prior findings [3], we assume that the daily average temperature (mesor) is unknown and generally inconstant. Let’s further assume that  is the input mesor-modeling signal that needs to be rated by the current readings simultaneously with the state vector  within the discrete model.

We offer herein a recurrent optimal filtration algorithm provided by study [4] for the estimation purposes – to compute the optimal state vector values for the model (including temperature) and evaluate the unknown mesor at any time moment based on the readings.

We developed special software in MATLAB language for the computer model design purposes, with a computer model working as follows. First we should set the known parameters of the model as specified above; fix a modeling interval , i.e. the readings per day taken every 5min; and then generate for every discrete moment  the Gaussian random values  and  with the zero mathematical expectation and preset co-variations  and , respectively. Having assumed that the ‘true’ mesor equals , we model next reading . Then we apply the prior estimated values , and current reading  to compute the current values ,  using the equations of the filtration algorithm [4].

The computer model test data are given on Figure hereunder, with the red circles representing the readings; solid black line – estimated body temperature; and the green line – estimated mesor.

Study findings and discussion. The model provides for the temperature estimate  at time moment  being equal to the summated estimated components of the state vector , i.e. . It is not always convenient, however, for the daily thermometric process modeling. The problem may be solved by the standard model with the reading pattern looking as . In this case the estimated temperature will equal the first component of the state vector , i.e. .

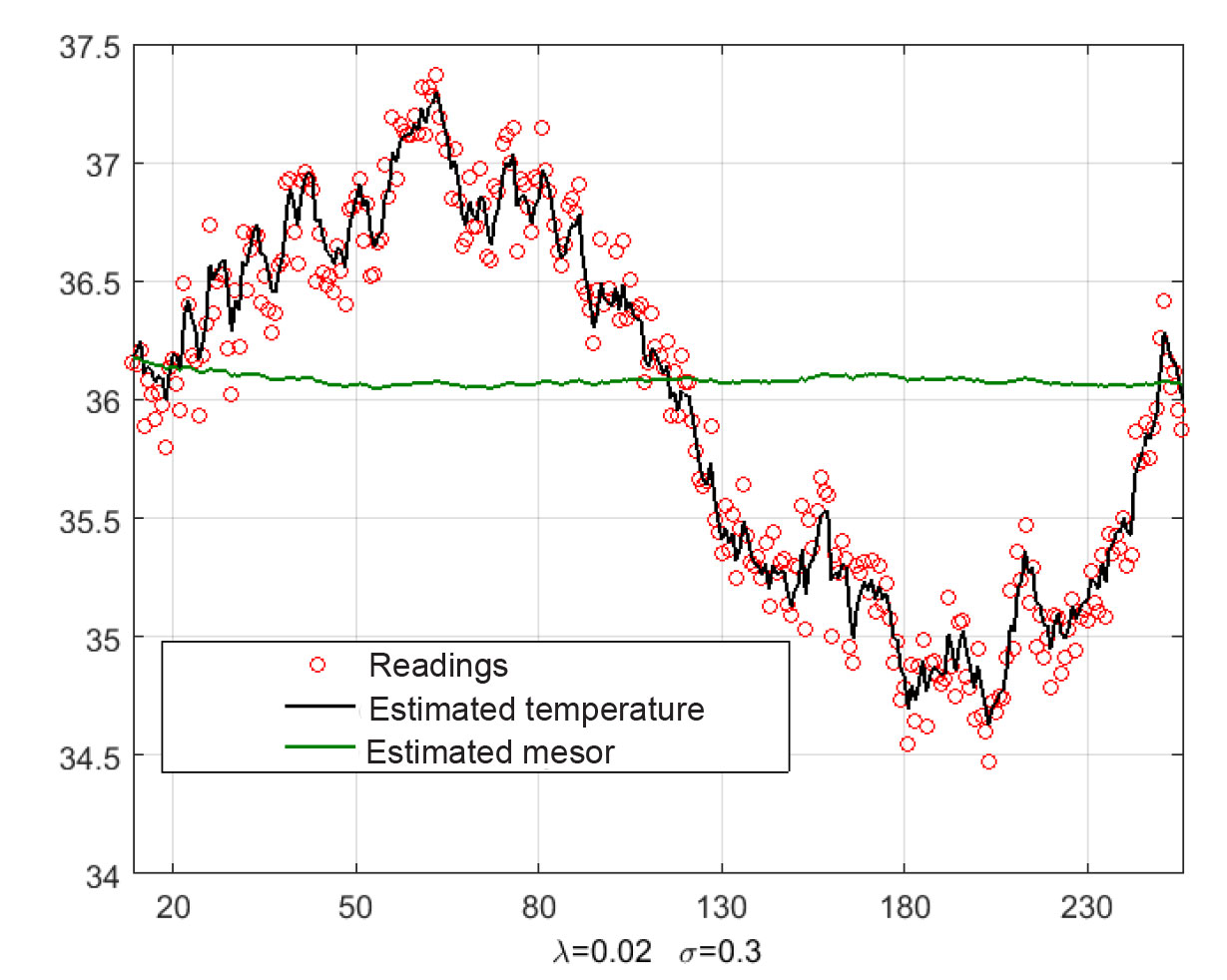
Figure 1.Computer model test data

It should be mentioned that one more solution for the simultaneous estimates of temperature and mesor (different from this one) is provided by the fourth-order model [7, 1, 3] that assumes an unknown control parameter as the additional component of the stage vector . This approach, however, overburdens the model and the relevant filtration algorithms by an extra dimension. We offer herein the state vector and the unknown discrete (linear stochastic systems) thermometric data input being estimated simultaneously, within the limited dimensions. The computer model testing experiment showed that the mathematical model fairly well represents the actual human biological circadian rhythms of a healthy human’s thermal homeostasis, with the temperature and mesor estimates made on a real-time basis using the current readings adjusted for the error rate of the thermometric equipment.

Conclusion. The third-order model with an unknown input offered herein was tested to fairly well represent the actual human biological circadian rhythms of the healthy human’s thermal homeostasis. The recurrent optimal filtration algorithm applied in the discrete linear stochastic system class with the unknown inputs makes it possible to simultaneously estimate the current temperatures and mesors based on a flow of momentary readings. The study findings may be applied to analyze the daily thermal homeostasis in healthy individuals.

References

1. Krolivetskaya Yu.M., Petrova E.S. Postroenie stokhasticheskikh modeley teplovogo gomeostaza cheloveka [Stochastic models of human thermal homeostasis]. Vestnik Astrakhan. gos. tekh. un-ta. Ser.: Upravlenie, vychisl. tekhn. inform, 2014, no. 1, pp. 140–152.
2. Nefedov V.P., Yasaytis A.A., Novoseltsev V.N. Gomeostaz na razlichnykh urovnyakh organizatsii biosistem [Homeostasis at different levels of organization of biosystems]. Novosibirsk: Nauka. Sib. branch, 1991. 232 p.
3. Tsyganova Yu.V. Ob odnoy modeli sutochnoy termometrii teplovogo gomeostaza cheloveka [Model of daily thermometry of human thermal homeostasis]. Fundamentalnye i prikladnye issledovaniya po prioritetnym napravleniyam bioekologii i biotekhnologii, sektsiya 'Matematicheskoe modelirovanie v bioekologii i biotekhnologii' ['Fundamental and applied research in priority areas of bioecology and biotechnology', section 'Mathematical modeling in bioecology and biotechnology'], The 2st Intern. on-line res.-practical conf. February 2015. Ulyanovsk: Ulyanov UlSPU. pp. 167–170.
4. Gillijns S.B. De Moor Unbiased minimum-variance input and state estimation for linear discrete-time systems with direct feedthrough. Automatica, vol. 43, 2007, pp. 934–937.
5. Kelly G. Body temperature variability (Part 1): a review of the history of body temperature and its variability due to site selection, biological rhythms, fitness, and aging. Altern. Med. Rev. 2006. Vol. 11, no. 4. P. 278–93.
6. Redfern P., Minors D., Waterhouse J. Circadian rhythms, jet lag, and chronobiotics: an overview. Chronobiol. Intern. 1994. No. 11. Р. 253– 256.
7. Semushin I.V., Tsyganova J.V., Skovikov A.G. Identification of a Simple Homeostasis Stochastic Model Based on Active Principle of Adaptation. Proceedings of International Conference 'Applied Stochastic Models and Data Analysis ASMDA 2013 & DEMOGRAPHICS 2013', 25–28 June 2013 Mataro (Barcelona), Spain. Barcelona, 2013. pp. 775–783.
8. Semushin I.V., Tsyganova J.V., Kulikova M.V. et al. Identification of Human Body Daily Temperature Dynamics via Minimum State Prediction Error Method Proceedings of ECC2016, European Control Conference (Aalborg, Denmark. June 29–July 1, 2016). IEEE, 2016.pp. 2429–2434.

Corresponding author: andrew.tsyganov@gmail.com

Abstract

Objective of the study was to revise the existing mathematical computation models for a daily thermal homeostasis in healthy individuals; and offer a new mathematical model with the discrete linear stochastic systems addressing the state space with unknown inputs and noisy measurements. The model variation vector includes tests of the body temperatures in discrete moments, with the mesor viewed as an the unknown input. We applied for the body temperature and mesor estimates an optimal discrete filtering algorithm with the state vector and unknown input being rated simultaneously. We developed for the purposes of the study application software in MATLAB language for computer modeling of the temperature curves and test process, to secure the arithmetic model parameters being estimated on an optimal basis. The study findings may be applied to analyze the daily thermal homeostasis in healthy individuals.