Dr.Hab., Professor V.I. Zagrevskiy^{1, 2}
Dr.Hab., Professor O.I. Zagrevskiy^2
1Mogilev State A. Kuleshov University, Mogilev, Belarus
²National Research Tomsk State University, Tomsk

Keywords: sport exercises, model, turn matrix, calculation experiment, biomechanical system.

Background. As things now stand in the modern sport science, competent management of the motor skill mastering process is virtually impossible unless supported by a profound knowledge of the sport exercise performance techniques that are being studied by modern and constantly improved research methods [1, 3, 6]. Since the sport exercise technique is a core subject for our studies of sport exercise biomechanics, the sets of research instruments to explore the human motor actions using modern information technologies are developed on the idea of the biomechanical research methods being harmonically combined with the rapidly progressing computer modelling technologies.

Visual reconstruction of the kinematic chain positions and orientations using the modern computer-graphics-based toolkits has always been a challenging task. This task is quite complicated even for the two-dimensional biomechanical system movement modelling and, naturally, much more complicated for geometric spatial modelling of biomechanical system movements. In addition to the difficulties of marker points (on joints) calculations for the athlete’s movements in space (with progressive and rotational movements of parts versus the axis of global coordinate system), the researcher must solve the problem of the biomechanical system’s kinematic chains being visualized and projected onto the coordinate plane of the monitor. This task effectively implies the ready biomechanical system’s spatial movement model being transformed into its planar (two-dimensional) simplified version. This task may be solved by methods of analytical and projective geometry [2]. It may be due to the serious computation difficulties in the attempts to solve these tasks that the modern physical exercise biomechanics has still failed to tackle the issue of a biomechanical system movement in space being visualized using the modern computer technologies.

As things now stand in the advanced research technologies in the motor action biomechanics, despite the reasonably informative processing methods being increasingly applied to optical movement registration data and processing, most of these methods are focused on two-dimensional presentations of athletic movements [3, 4, 6] and it might be the reason for the further progress being quite limited. It should be noted that most of the planar and even more spatial kinematic chains characteristic of the most sport exercises have not been studied as yet. Therefore, there is a need to improve the newly developed advanced technical tools to solve a variety of direct and reverse tasks of modern spatial kinematics and dynamics of sport exercises.

Objective of the study was to develop a technological foundation for mathematical tools and software to visualize the preset spatial position and orientation of a biomechanical system.

Study results and discussion. The study was based on the results of planar and spatial geometric transformations of moving objects. These were the biomechanical system segments that were used as the moving objects under the study, and geometric primitive forms like spheres, cubes and parallelepipeds with a variety of linear specifications were used to model these segments.

Planar geometric transformations: rotation matrices

Spatial positions of the biomechanical system segments in an absolute (immovable) Cartesian coordinate system (CCS) may be described using methods of matrix algebra [5].

Elementary rotation matrix: Rotation of a modelled object around each axis of the CCS may be described by a specific elementary rotation matrix (See Figure 1).

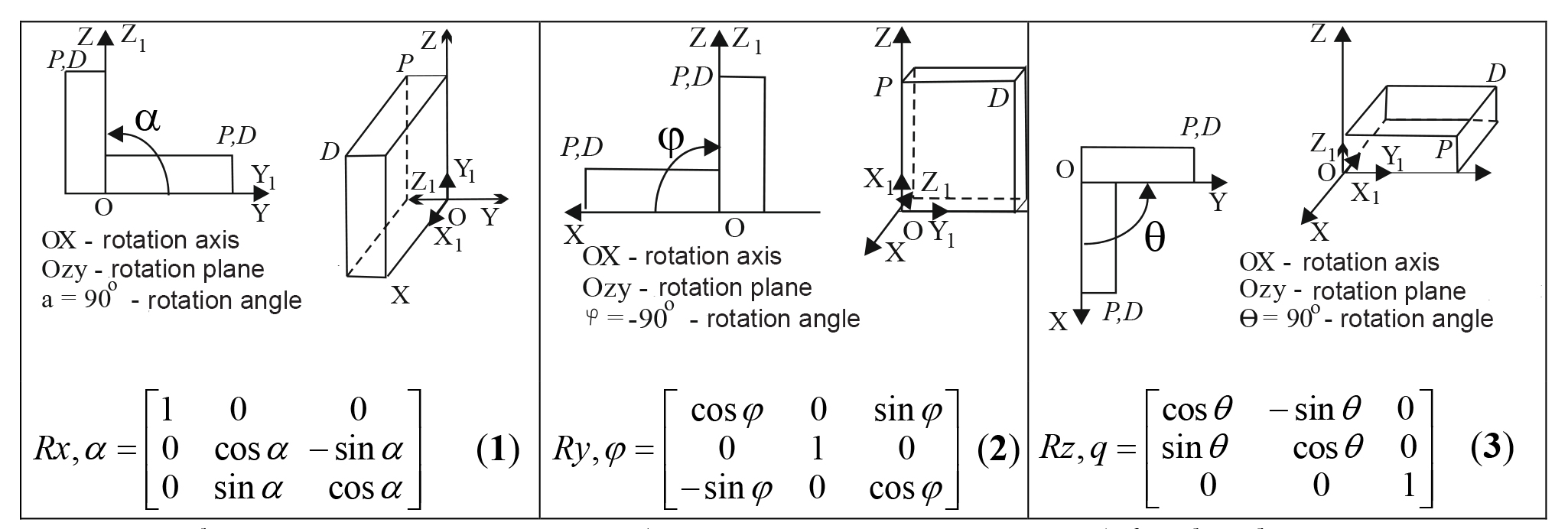
Figure 1. Elementary rotation matrices (– 1;  – 2; – 3) for the object rotation around each of the axes (OX, OY, OZ) of the Cartesian coordinate system by angles, ,

Spatial geometric transformations: complex rotation matrices

Kinematic analysis is further complicated in case of biomechanical system movement in space being subject to the study, as opposed to the planar one.

Complex rotation matrix: A sequence of ultimate rotations around the main axes of the OXYZ system may be described by the elementary rotation matrices being multiplied [5]. For example, for the sequence of rotations initially performed by  angle around OX axis and further by angle around OZ axis and, finally, by  angle around OY axis, the resultant rotation matrix will have the following form:

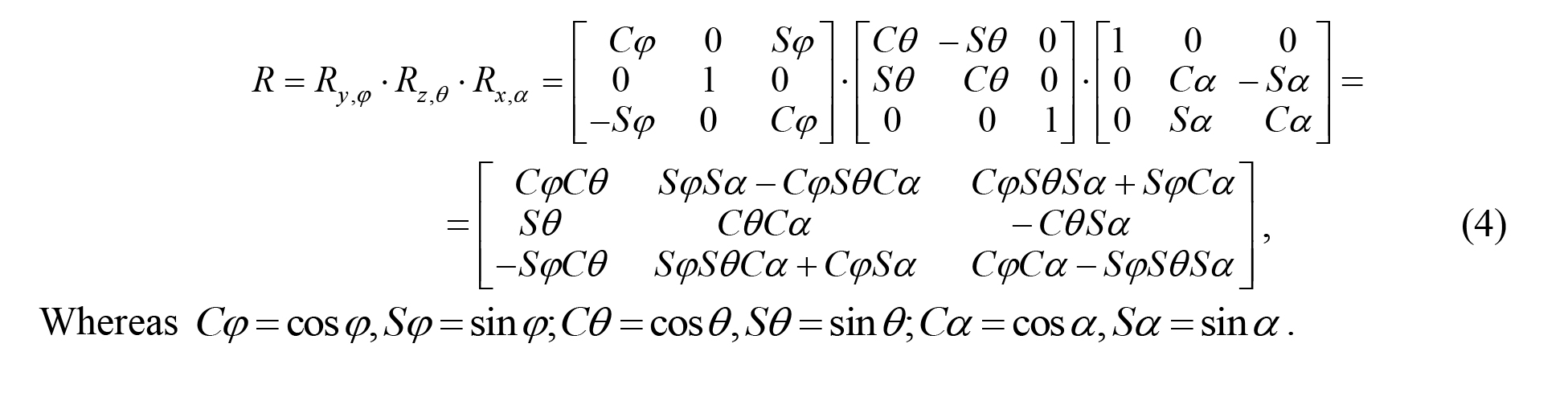
It should be noted that the resultant ultimate rotation matrix will depend on the sequence of rotations since the matrices multiplying operation is non-commutative. Coloration of the parallelepiped faces was made hereunder using a sequential coloration method [2], for the reason that this method secures the necessary face changeover sequence and correct spatial animation of the parallelepiped. We used a special application software to run a series of computation experiments designed to model the rotation movements of the object in differently oriented local coordinate systems connected with the rotating body. The preset positions and orientations of the object were geared to simulate positions of the athlete’s body segments in space (see Figure 2). Note that the ultimate rotation angles are printed by the relevant colours; the rotation goes clockwise; and the rotation axis goes through the mass centre of the model.

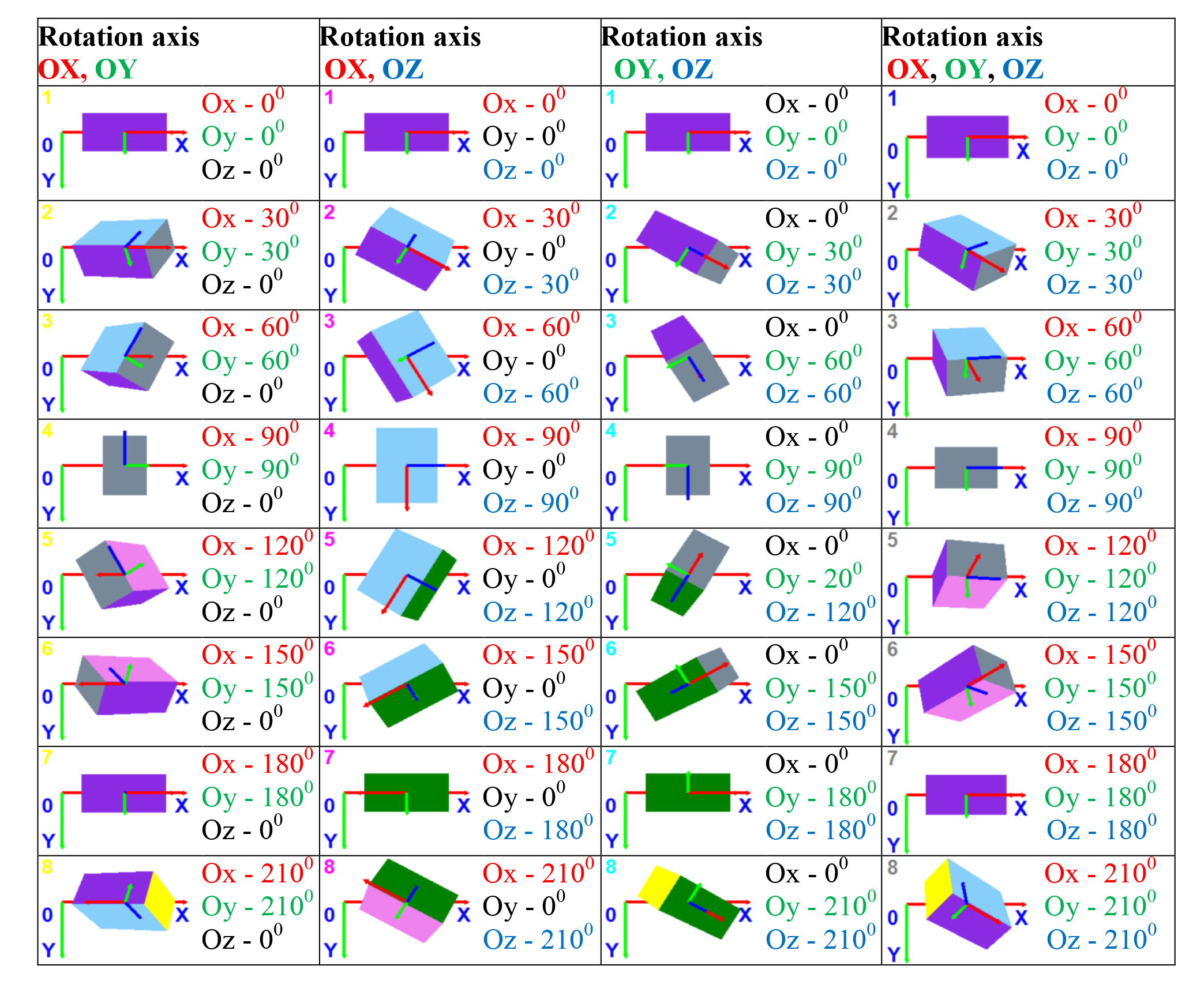
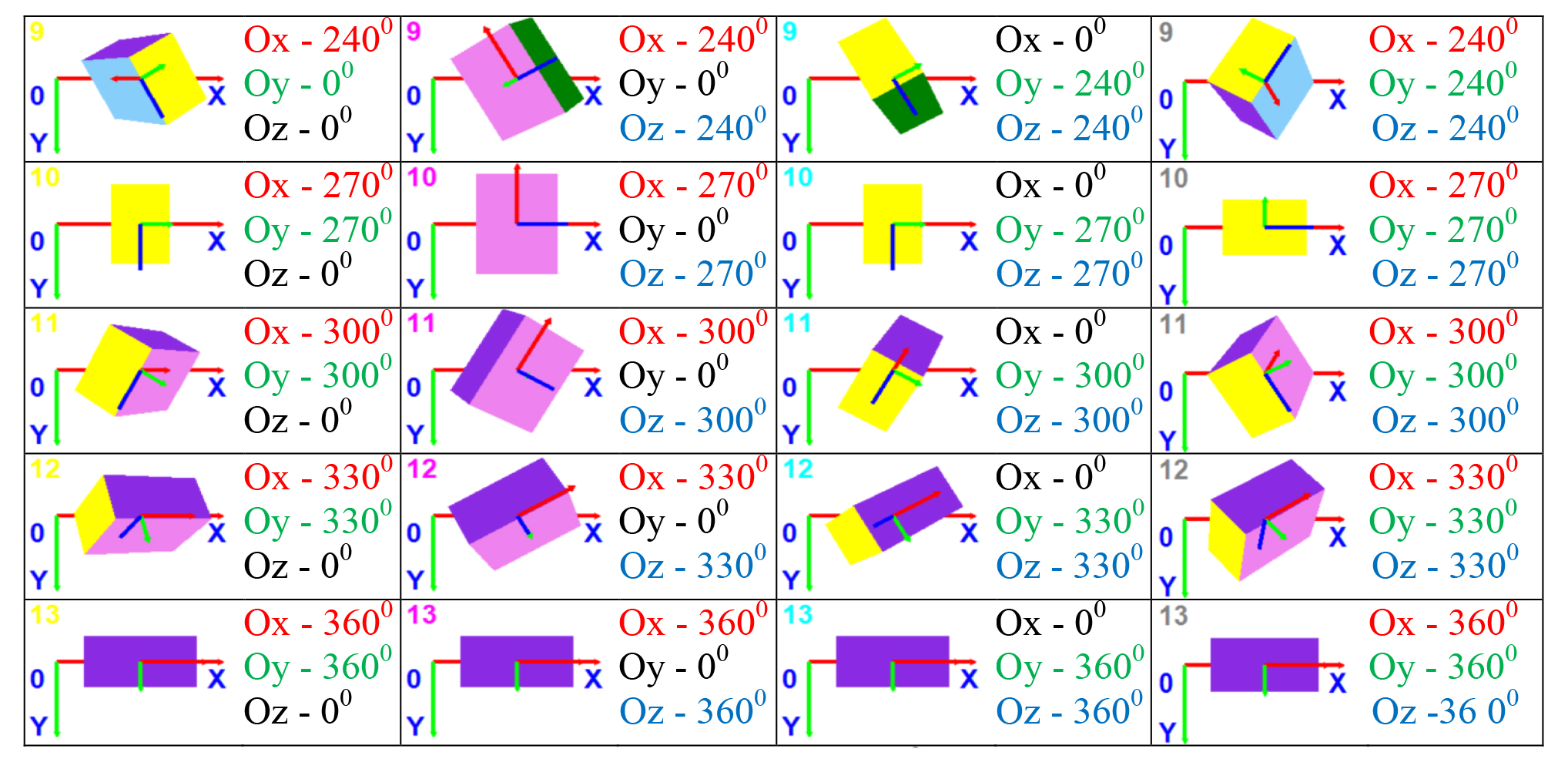
Figure 2. Spatial rotation of the model with a step of 30⁰ around axes (OX, OY),

(OX, OZ), (OY, OZ), (OX, OY, OZ) of the Cartesian coordinate system

To solve the problem subject to the study, we used a computer software of our own design made in algorithmic language Visual Basic 2010 Express within the i Visual Studio 2013 integrated design toolkit. The computation experiment resulted in the spatial positions of the model being found in its sequential rotation around axes OX, OY (with the first series of the computation experiments given in Figure 2, column 1) with a step of 30⁰. Given in columns 2, 3 and 4 of the above Figure are the results of the computation experiment with the model being rotated around the Cartesian coordinate system axes (OX, OZ), (OY, OZ), (OX, OY, OZ).

Conclusion. The study resulted in the fundamental mathematical tools and computer software being developed for modelling segments of a moving biomechanical system by primitive geometrical forms like spheres, cubes and parallelepipeds. We believe it would be highly promising for further works to develop applications of the newly research technology that could give the potential means to explore directly spatial kinematic couples and links of a biomechanical system to solve a variety of direct and reverse tasks of the sport movement biomechanics.    

References

1. Gaverdovskiy Yu.K. Obuchenie sportivnym uprazhneniyam. Biomekhanika. Metodologiya. Didaktika (Teaching Sport Exercises. Biomechanics. Methodology. Didactics) / Yu.K. Gaverdovskiy. – Moscow: Fizkul'tura i sport, 2007. – 912 p.
2. Demin A.Yu. Osnovy komp'yuternoy grafiki: ucheb. posobie (Fundamentals of Computer Graphics: study guide) / A.Yu. Demin; Tomsk Polytechnic University. - Tomsk: Publishing house of Tomsk Polytechnic University, 2011. – 191 p.
3. Zagrevskiy V.I. Vliyanie upravlyayushchikh dvizheniy v sustavakh sportsmena na tekhniku gimnasticheskogo uprazhneniya «perelet Tkacheva» na perekladine (Influence of control joint movements on technique of gymnastic bar exercise "reverse-hecht staddle catch") / V.I. Zagrevskiy, V.G. Shilko, V.O. Zagrevskiy, I.L. Lukashkova // Vestnik Tomskogo gosudarstvennogo universiteta (Bulletin of Tomsk Polytechnic University). – 2012. – № 361. – P. 135–139.
4. Zagrevskiy O.I. Tekhnika «bol'shogo oborota nazad iz stoyki na rukakh v stoyku na rukakh na parallel'nykh brus'yakh» na etape formirovaniya dvigatel'nogo umeniya i navyka (technique of "giant swing backward from handstand into handstand on parallel bars" at motor ability and skill formation stage) / O.I. Zagrevskiy, V.I. Zagrevskiy // Teoriya i praktika fizicheskoy kultury. – 2015. – № 7. – P. 23–25.
5. Fu K. Robototekhnika (Robotics: Trans. from English) / K. Fu, R. Gonsales, K. Li. – Moscow: Mir, 1989. – 624 p.
6. Sherin V.S. Rol' biomekhaniki v sovershenstvovanii tekhniki gimnasticheskikh uprazhneniy (Biomechanics in gymnastic exercise technique enhancement) / V.S. Sherin // Fizicheskaya kul'tura, zdravookhranenie i obrazovanie: mater. Vseros. nauch.-prakt. konf. pamyati V.S. Pirusskogo, Tomsk (Physical education, health care and education: Proc. res.-prac. conf. in memory of V.S. Pirusskiy), Tomsk, November 20-21 2008). – Tomsk, 2008. P. 161–163.

Corresponding author: kapil@yandex.ru

Abstract
Objective of the study was to develop a technological foundation for mathematical and software tools to visualize the preset spatial position and orientation of a biomechanical system. The study results showed that segments of a biomechanical system may be modelled by a variety of primitive geometrical forms like spheres, cubes and parallelepipeds. Using the tree-dimensional rotation of a parallelepiped for the case study, we found different positions of the local coordinate system and designed the relevant frame model of the parallelepiped movement in the absolute coordinate sys-tem. The rotating subject was visualized with a step of 300 within the rotation angle variation range (by each axis of the Cartesian coordinate system) from 00 (starting position of the model) to 3600 (finishing position of the model). The three-dimensional rotation effect was achieved by coloration of the parallelepiped faces. The rotation process was described by the elementary and complex rota-tion matrices supported by the relevant mathematical expressions. In further studies, we are going to adapt the frame computer modelling of the human body segments’ spatial variations to the kine-matic couples and kinematic chains of a biomechanical system. A successful solution of the problem will make it possible to model the sport exercise performance techniques both in the two- and three-dimensional formats.